Contents

1 Функция fractile(выражение, fractile)
- 1.1 Теория по квантилю в статистике
- 1.2 Практика — нахождение квантиля в QlikView
2 Функция kurtosis([distinct ] выражение)
- 2.1 Теория по куртозису в статистике
- 2.2 Практика — нахождение куртозиса в QlikView
3 Функция correl(выражение_x, выражение_y)
- 3.1 Теория по корреляции в статистике
- 3.2 Практика — нахождение коэффициента корреляции в QlikView
4 Функция avg([distinct] выражение)
5 Функция stdev([distinct] выражение)
- 5.1 Теория по стандартному отклонению в статистике
- 5.2 Практика — нахождение стандартного отклонения в QlikView
6 Функция skew([ distinct] выражение)
- 6.1 Теория по асимметрии в статистике
- 6.2 Практика — нахождение коэффициента асимметрии в QlikView
7 Функция median (выражение)
- 7.1 Теория по медиане в статистике
- 7.2 Практика — нахождение медианы в QlikView
8 Функция sterr ([distinct] выражение)
- 8.1 Теория по стандартной ошибке в статистике
- 8.2 Практика — нахождение стандартной ошибки в QlikView
9 Функция steyx (выражение_y, выражение_x)
10 Функция linest_m (выражение_y, выражение_x [, y0 [, x0 ]])
- 10.1 Теория по линейной регрессии
- 10.2 Практика — построение трендов линейной регрессии в QlikView
11 Фукнция linest_b (выражение_y, выражение_x [, y0 [, x0 ]])
12 Функция linest_r2 (выражение_y, выражение_x [, y0 [, x0 ]])
13 Функция linest_sem (выражение_y, выражение_x [, y0 [, x0 ]])
14 Функция linest_seb (выражение_y, выражение_x [, y0 [, x0 ]])
15 Функция linest_sey (выражение_y, выражение_x [, y0 [, x0 ]])
16 Функция linest_df (выражение_y, выражение_x [, y0 [, x0 ]])
17 Функция linest_f (выражение_y, выражение_x [, y0 [, x0 ]])
18 Функция linest_ssreg (выражение_y, выражение_x [, y0 [, x0 ]])
19 Функция linest_ssresid (выражение_y, выражение_x [, y0 [, x0 ]])

В данной статье будут рассмотрены статистические функции, которые доступны в QlikView. С их помощью можно рассчитывать статистические показатели, а также строить линейные тренды на основе исторических данных. Функции достаточно простые и явно уступают по возможностям статистическим продуктам на основе языка программирования R, но для проектирования простых статистических моделей подходят. В любом случае всегда можно интегрировать Open-Source продукт с QlikView и получить отличную аналитическую платформу на статистических данных.

Функция fractile(выражение, fractile)

Теория по квантилю в статистике

Квантиль – это значение, которое ряд случайных величин не превышает с заданной вероятностью.
Квантиль порядка t, q_t:
P(у_i<=q_t)=t
Например: Квантиль порядка 10% для y_i — такое число q_0.1, что вероятность того, что y_i окажется меньше этого числа, равна 10%.

Практика — нахождение квантиля в QlikView

Функция fractile(выражение, fractile) возвращает квантиль выражения для ряда записей, которые определены выражением group by (агрегация значений по группам).
Пример:

Load Class, fractile( Grade, 0.75 ) as F from abc.csv group by Class;

1	Load Class, fractile( Grade, 0.75 ) as F from abc.csv group by Class;

Функция kurtosis([distinct ] выражение)

Теория по куртозису в статистике

Куртозис (kurtosis) — это показатель, который отражает остроту вершины и толщину хвостов одномерного распределения.
Куртозис (kurtosis) или эксцесс – это четвертый центральный момент распределения отклонений от среднего, нормированный дисперсией.

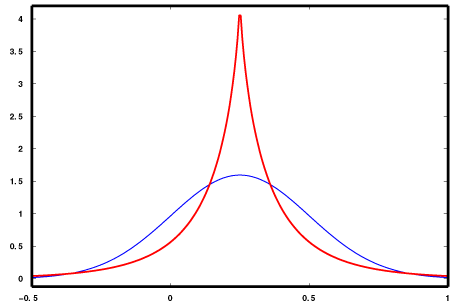
Синяя кривая – нормальное распределение (куртозис нормального распределения вне зависимости от математического ожидания и стандартного отклонения равен 3).
Красная кривая – имеет положительный эксцесс/куртозис больше 3.

Практика — нахождение куртозиса в QlikView

Функция kurtosis([distinct ] выражение) возвращает эксцесс выражения для ряда записей, которые определены выражением group by. Если слово distinct указано перед выражением, то все дубликаты будут проигнорированы.
Пример:

Load Month, kurtosis(Sales) as SalesKurtosis from abc.csv group by Month;

1	Load Month, kurtosis(Sales) as SalesKurtosis from abc.csv group by Month;

Функция correl(выражение_x, выражение_y)

Теория по корреляции в статистике

Корреляция — коэффициент, который характеризует взаимозависимость двух или нескольких случайных величин. Суть ее заключается в том, что при изменении значения одной переменной происходит закономерное изменение (уменьшение или увеличение) другой переменной.
Корреляция не говорит о причинно-следственных связях, она говорит лишь о взаимосвязанности рассматриваемых параметров, причем в данной конкретной выборке, в другой выборке мы можем не наблюдать полученные корреляции.
Коэффициент корреляции варьируется в пределах от -1 (отрицательная корреляция) до +1 (положительная корреляция). Если коэффициент корреляции равен 0 то, это говорит об отсутствии корреляционных связей между переменными. Если коэффициент корреляции ближе к 1 или -1, то это говорит о сильной корреляции, а если ближе к 0 — о слабой корреляции.
При положительной корреляции увеличение (или уменьшение) значений одной переменной ведет к закономерному увеличению (или уменьшению) другой переменной, т.е. взаимосвязи типа увеличение-увеличение (уменьшение-уменьшение).
При отрицательной корреляции увеличение (или уменьшение) значений одной переменной ведет к закономерному уменьшению (или увеличению) другой переменной, т.е. взаимосвязи типа увеличение-уменьшение (уменьшение-увеличение).

Практика — нахождение коэффициента корреляции в QlikView

Функция correl(выражение_x, выражение_y) возвращает агрегированный коэффициент корреляции для серии координат, представленных парными номерами в выражение_x и выражение_y с итерацией для ряда записей, которые определены выражением group by. Текстовые, нулевые и отсутствующие значения в какой-либо или обеих частях пары данных приводят к игнорированию всей пары данных.
Пример:

Load Month, correl(X,Y) as CC from abc.csv group by Month;

1	Load Month, correl(X,Y) as CC from abc.csv group by Month;

Функция avg([distinct] выражение)

Возвращает среднее значение выражение для ряда записей, которые определены выражением group by. Если слово distinct указано перед выражением, все дубликаты будут проигнорированы.
Пример:

Load Month, avg(Sales) as AverageSalesPerMonth from abc.csv group by Month;

1	Load Month, avg(Sales) as AverageSalesPerMonth from abc.csv group by Month;

Функция stdev([distinct] выражение)

Теория по стандартному отклонению в статистике

Стандартное отклонение — это показатель рассеивания значений случайной величины относительно её математического ожидания, является хорошим индикатором изменчивости (плюс-минус столько-то от среднего).
Чем больше значение стандартного отклонения, тем больше разброс.

Практика — нахождение стандартного отклонения в QlikView

Фукнция stdev ([distinct] выражение) возвращает стандартное отклонение выражения для ряда записей, которые определены выражением group by. Если слово distinct указано перед выражением, все дубликаты будут проигнорированы.
Пример:

Load Month, stdev(Sales) as SalesStandardDeviation from abc.csv group by Month;

1	Load Month, stdev(Sales) as SalesStandardDeviation from abc.csv group by Month;

Функция skew([ distinct] выражение)

Теория по асимметрии в статистике

Коэффициент асимметрии — величина, характеризующая асимметрию распределения данной случайной величины. Асимметрия — это числовое отображение степени отклонения графика распределения ряда значений от симметричного графика распределения.
Коэффициент асимметрии положителен, если правый хвост распределения длиннее левого, и отрицателен, если левый хвост распределения длиннее правого. Если распределение симметрично относительно математического ожидания, то его коэффициент асимметрии равен нулю.

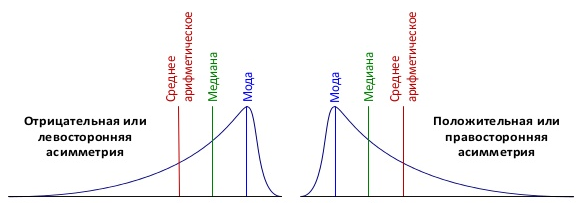
Практика — нахождение коэффициента асимметрии в QlikView

Функция skew([ distinct] выражение) возвращает асимметрию выражения для ряда записей, которые определены выражением group by. Если слово distinct указано перед выражением, все дубликаты будут проигнорированы.
Пример:

Load Month, skew(Sales) as SalesSkew from abc.csv group by Month;

1	Load Month, skew(Sales) as SalesSkew from abc.csv group by Month;

Функция median (выражение)

Теория по медиане в статистике

Медиана (от лат. mediana — середина) 50-й перцентиль или квантиль 0,5 — статистика, которая делит ранжированную совокупность (вариационный ряд выборки) на две равные части: 50 % «нижних» членов ряда данных будут иметь значение признака не больше, чем медиана, а «верхние» 50 % — значения признака не меньше, чем медиана.
Медиана — это значение выборки, которое делит все значения выборки пополам. Расчет медианы проводится следующим образом: все значения выстраиваются от наименьшего до наибольшего. Центральное значение ряда является медианой (медиана буквально означает середину).

Практика — нахождение медианы в QlikView

Функция median(выражение) возвращает агрегированную медиану выражения для ряда записей, которые определены выражением group by.
Пример:

Load Class, Median(Grade) as MG from abc.csv group by Class;

1	Load Class, Median(Grade) as MG from abc.csv group by Class;

Функция sterr ([distinct] выражение)

Теория по стандартной ошибке в статистике

Стандартная ошибка – это стандартное отклонение оценок, которые будут получены при многократной случайной выборке данного размера из одной и той же совокупности. Стандартная ошибка – это убывающая функция объема выборки: чем меньше стандартная ошибка, тем более достоверной является оценка. Может вычисляться для любых выборочных статистик, используется при построении соответствующих доверительных интервалов и статистической проверке гипотез.

Стандартная ошибка средней измеряет изменчивость или отклонение средних значений выборок от истинной (популяционной или генеральной) средней.

Практика — нахождение стандартной ошибки в QlikView

Функция sterr ([distinct] выражение) возвращает агрегированную стандартную ошибку (stdev/sqrt(n)) для серии значений, представленных выражением с итерацией для ряда записей, которые определены выражением group by. Текстовые, нулевые и отсутствующие значения будут игнорироваться. Если слово distinct указывается до аргументов функции, все дубликаты, возникшие в результате оценки аргументов функции, будут проигнорированы.
Пример:

Load Key, sterr(X) as Z from abc.csv group by Key;

1	Load Key, sterr(X) as Z from abc.csv group by Key;

Функция steyx (выражение_y, выражение_x)

Функция steyx (выражение_y, выражение_x) возвращает агрегированную стандартную ошибку прогнозируемого y-значения для каждого x-значения в регрессии для серии координат, представленных парными номерами в выражении_x и выражении_y с итерацией для ряда записей, которые определены выражением group by. Текстовые, нулевые и отсутствующие значения в какой-либо или обеих частях пары данных приводят к игнорированию всей пары данных.
Пример:

Load Key, steyx(Y,X) as Z from abc.csv group by Key;

1	Load Key, steyx(Y,X) as Z from abc.csv group by Key;

Функция linest_m (выражение_y, выражение_x [, y0 [, x0 ]])

Теория по линейной регрессии

Линейная регрессия (англ. Linear regression) — используемая в статистике регрессионная модель зависимости одной (объясняемой, зависимой) переменной y от другой или нескольких других переменных (факторов, регрессоров, независимых переменных) x с линейной функцией зависимости.

Практика — построение трендов линейной регрессии в QlikView

Функция linest_m (выражение_y, выражение_x [, y0 [, x0 ]]) возвращает агрегированное значение m (пересечение) линейной регрессии, определенной уравнением y=mx+b, для серии координат, представленных парными номерами в выражении_x и выражении_y с итерацией для ряда записей, которые определены выражением group by. Текстовые, нулевые и отсутствующие значения в какой-либо или обеих частях пары данных приводят к игнорированию всей пары данных.
Дополнительное значение y0 и x0 можно указать путем принудительного прохождения линии регрессии через ось y в определенной точке. Указав y0 и x0, можно инициировать принудительное прохождение линии регрессии через одну фиксированную координату.
Если значения y0 и x0 не указаны, для вычисления функции требуются хотя бы две допустимые пары данных. Если y0 и x0 указаны, используется одна пара данных.
Пример:

Load Key, linest_m(Y,X) as Z from abc.csv group by Key;

1	Load Key, linest_m(Y,X) as Z from abc.csv group by Key;

Фукнция linest_b (выражение_y, выражение_x [, y0 [, x0 ]])

Функция linest_b (выражение_y, выражение_x [, y0 [, x0 ]]) возвращает агрегированное значение b (y-intercept) линейной регрессии, определенной уравнением y=mx+b, для серии координат, представленных парными номерами в выражении_x и выражении_y с итерацией для ряда записей, которые определены выражением group by. Текстовые, нулевые и отсутствующие значения в какой-либо или обеих частях пары данных приводят к игнорированию всей пары данных.
Дополнительное значение y0 и x0 можно указать путем принудительного прохождения линии регрессии через ось y в определенной точке. Указав y0 и x0, можно инициировать принудительное прохождение линии регрессии через одну фиксированную координату.
Если значения y0 и x0 не указаны, для вычисления функции требуются хотя бы две допустимые пары данных. Если y0 и x0 указаны, используется одна пара данных.
Пример:

Load Key, linest_b(Y,X) as Z from abc.csv group by Key;

1	Load Key, linest_b(Y,X) as Z from abc.csv group by Key;

Функция linest_r2 (выражение_y, выражение_x [, y0 [, x0 ]])

Функция linest_r2 (выражение_y, выражение_x [, y0 [, x0 ]]) возвращает агрегированное значение r2 (коэффициент детерминации) линейной регрессии, определенной уравнением y=mx+b, для серии координат, представленных парными номерами в выражении_x и выражении_y с итерацией для ряда записей, которые определены выражением group by.
Текстовые, нулевые и отсутствующие значения в какой-либо или обеих частях пары данных приводят к игнорированию всей пары данных.
Дополнительное значение y0 и x0 можно указать путем принудительного прохождения линии регрессии через ось y в определенной точке. Указав y0 и x0, можно инициировать принудительное прохождение линии регрессии через одну фиксированную координату.
Если значения y0 и x0 не указаны, для вычисления функции требуются хотя бы две допустимые пары данных. Если y0 и x0 указаны, то используется одна пара данных.
Пример:

Load Key, linest_r2(Y,X) as Z from abc.csv group by Key;

1	Load Key, linest_r2(Y,X) as Z from abc.csv group by Key;

Функция linest_sem (выражение_y, выражение_x [, y0 [, x0 ]])

Функция linest_sem (выражение_y, выражение_x [, y0 [, x0 ]]) возвращает агрегированную стандартную ошибку значения m линейной регрессии, определенной уравнением y=mx+b для серии координат, представленных парными номерами в выражении_x и выражении_y, с итерацией для ряда записей, которые определены выражением group by. Текстовые, нулевые и отсутствующие значения в какой-либо или обеих частях пары данных приводят к игнорированию всей пары данных.
Дополнительное значение y0 и x0 можно указать путем принудительного прохождения линии регрессии через ось y в определенной точке. Указав y0 и x0, можно инициировать принудительное прохождение линии регрессии через одну фиксированную координату.
Если значения y0 и x0 не указаны, для вычисления функции требуются хотя бы две допустимые пары данных. Если y0 и x0 указаны, используется одна пара данных.
Пример:

Load Key, linest_sem(Y,X) as Z from abc.csv group by Key;

1	Load Key, linest_sem(Y,X) as Z from abc.csv group by Key;

Функция linest_seb (выражение_y, выражение_x [, y0 [, x0 ]])

Функция linest_seb (выражение_y, выражение_x [, y0 [, x0 ]]) возвращает агрегированную стандартную ошибку значения b линейной регрессии, определенной уравнением y=mx+b для серии координат, представленных парными номерами в выражении_x и выражении_y, с итерацией для ряда записей, которые определены выражением group by. Текстовые, нулевые и отсутствующие значения в какой-либо или обеих частях пары данных приводят к игнорированию всей пары данных.
Дополнительное значение y0 и x0 можно указать путем принудительного прохождения линии регрессии через ось y в определенной точке. Указав y0 и x0, можно инициировать принудительное прохождение линии регрессии через одну фиксированную координату.
Если значения y0 и x0 не указаны, для вычисления функции требуются хотя бы две допустимые пары данных. Если y0 и x0 указаны, используется одна пара данных.
Пример:

Load Key, linest_seb(Y,X) as Z from abc.csv group by Key;

1	Load Key, linest_seb(Y,X) as Z from abc.csv group by Key;

Функция linest_sey (выражение_y, выражение_x [, y0 [, x0 ]])

Функция linest_sey (выражение_y, выражение_x [, y0 [, x0 ]]) возвращает агрегированную стандартную ошибку оценки y линейной регрессии, определенной уравнением y=mx+b для серии координат, представленных парными номерами в выражении_x и выражении_y, с итерацией для ряда записей которые определены выражением group by. Текстовые, нулевые и отсутствующие значения в какой-либо или обеих частях пары данных приводят к игнорированию всей пары данных.
Дополнительное значение y0 и x0 можно указать путем принудительного прохождения линии регрессии через ось y в определенной точке. Указав y0 и x0, можно инициировать принудительное прохождение линии регрессии через одну фиксированную координату.
Если значения y0 и x0 не указаны, для вычисления функции требуются хотя бы две допустимые пары данных. Если y0 и x0 указаны, используется одна пара данных.
Пример:

Load Key, linest_sey(Y,X) as Z from abc.csv group by Key;

1	Load Key, linest_sey(Y,X) as Z from abc.csv group by Key;

Функция linest_df (выражение_y, выражение_x [, y0 [, x0 ]])

Функция linest_df (выражение_y, выражение_x [, y0 [, x0 ]]) возвращает агрегированную степень свободы линейной регрессии, определенной уравнением y=mx+b, для серии координат, представленных парными номерами в выражении_x и выражении_y, с итерацией для ряда записей, которые определены выражением group by. Текстовые, нулевые и отсутствующие значения в какой-либо или обеих частях пары данных приводят к игнорированию всей пары данных.
Дополнительное значение y0 и x0 можно указать путем принудительного прохождения линии регрессии через ось y в определенной точке. Указав y0 и x0, можно инициировать принудительное прохождение линии регрессии через одну фиксированную координату.
Если значения y0 и x0 не указаны, для вычисления функции требуются хотя бы две допустимые пары данных. Если y0 и x0 указаны, используется одна пара данных.
Пример:

Load Key, linest_df(Y,X) as Z from abc.csv group by Key;

1	Load Key, linest_df(Y,X) as Z from abc.csv group by Key;

Функция linest_f (выражение_y, выражение_x [, y0 [, x0 ]])

Функция linest_f (выражение_y, выражение_x [, y0 [, x0 ]]) возвращает агрегированную статистику F(r2/(1-r2)) линейной регрессии, определенной уравнением y=mx+b, для серии координат, представленных парными номерами в выражении_x и выражении_y, с итерацией для ряда записей, которые определены выражением group by. Текстовые, нулевые и отсутствующие значения в какой-либо или обеих частях пары данных приводят к игнорированию всей пары данных.
Дополнительное значение y0 и x0 можно указать путем принудительного прохождения линии регрессии через ось y в определенной точке. Указав y0 и x0, можно инициировать принудительное прохождение линии регрессии через одну фиксированную координату.
Если значения y0 и x0 не указаны, для вычисления функции требуются хотя бы две допустимые пары данных. Если y0 и x0 указаны, используется одна пара данных.
Пример:

Load Key, linest_f(Y,X) as Z from abc.csv group by Key;

1	Load Key, linest_f(Y,X) as Z from abc.csv group by Key;

Функция linest_ssreg (выражение_y, выражение_x [, y0 [, x0 ]])

Функция linest_ssreg (выражение_y, выражение_x [, y0 [, x0 ]]) возвращает агрегированную сумму регрессии квадратов регрессии, определенной уравнением y=mx+b, для серии координат, представленных парными номерами в выражении_x и выражении_y, с итерацией для ряда записей, которые определены выражением group by. Текстовые, нулевые и отсутствующие значения в какой-либо или обеих частях пары данных приводят к игнорированию всей пары данных.
Дополнительное значение y0 и x0 можно указать путем принудительного прохождения линии регрессии через ось y в определенной точке. Указав y0 и x0, можно инициировать принудительное прохождение линии регрессии через одну фиксированную координату.
Если значения y0 и x0 не указаны, для вычисления функции требуются хотя бы две допустимые пары данных. Если y0 и x0 указаны, используется одна пара данных.
Пример:

Load Key, linest_ssreg(Y,X) as Z from abc.csv group by Key;

1	Load Key, linest_ssreg(Y,X) as Z from abc.csv group by Key;

Функция linest_ssresid (выражение_y, выражение_x [, y0 [, x0 ]])

Функция linest_ssresid (выражение_y, выражение_x [, y0 [, x0 ]]) возвращает агрегированную остаточную сумму квадратов регрессии, определенной уравнением y=mx+b, для серии координат, представленных парными номерами в выражении_x и выражении_y, с итерацией для ряда записей, которые определены выражением group by. Текстовые, нулевые и отсутствующие значения в какой-либо или обеих частях пары данных приводят к игнорированию всей пары данных.
Дополнительное значение y0 и x0 можно указать путем принудительного прохождения линии регрессии через ось y в определенной точке. Указав y0 и x0, можно инициировать принудительное прохождение линии регрессии через одну фиксированную координату.
Если значения y0 и x0 не указаны, для вычисления функции требуются хотя бы две допустимые пары данных. Если y0 и x0 указаны, используется одна пара данных.
Пример:

Load Key, linest_ssresid(Y,X) as Z from abc.csv group by Key;

1	Load Key, linest_ssresid(Y,X) as Z from abc.csv group by Key;